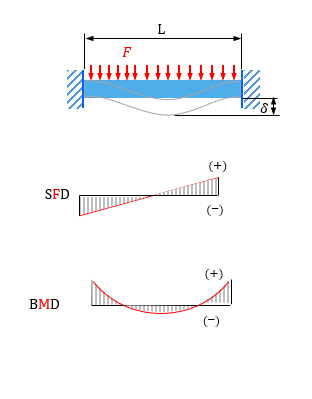
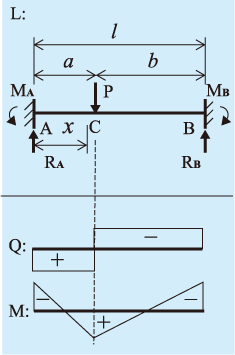
はり公式集p2 強度計算・実践への一歩 単径間・はり公式集 等分布荷重(部分/満載) → 他: 集中荷重 ・ 三角分布荷重 ・ モーメント荷重 梁,荷重図,SFD,BMD 反力RA, せん断力F, 端モーメントMA, 曲げモーメントM, たわみ角i, たわみy 式算出 (計算式の誘導) 固定 両端固定部分等分布荷重梁 の計算 部分等分布荷重両端固定梁の計算式をNASAの資料より抽出してみました。 原典:AFFDLTR6942_AUG1969 画像をクリックすると拡大表示されます。 By msudo 時刻 水曜日, 11月 18,Cb 間では負ですね。したがって、sfd は図3 のようになります。qac = r1 はac 間に働くせん断力、 qcb = −r2(= r1 −p) はcb 間に働くせん断力になります。 0 r1 () r2 () a c b p 図3 sfd
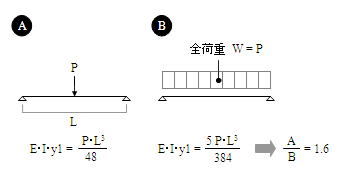
梁のたわみ量の計算について
両端固定梁 等分布荷重 モーメント
両端固定梁 等分布荷重 モーメント-その他荷重(kN/m2) ─── ─── ─── 底 版 自 重 上 面 荷 重 その他荷重(kN) ─── ─── ─── 32 側壁解析方法 側壁解析方法 備 考 水平応力解析 三辺固定スラブ法 両端固定梁+三辺固定版 ケース名 等変分布荷重 等分布荷重 備 考図の等分布荷重wが作用する片持ち梁の場合に、梁の断面形状は辺の長さaの正方形として、 (1)せん断力、曲げモーメントの式を求め、 (2)曲げモーメントの最大値を求め、生ずる最大応力を求める。 (3)たわみの式を求め、最大たわみδmaxを求める。
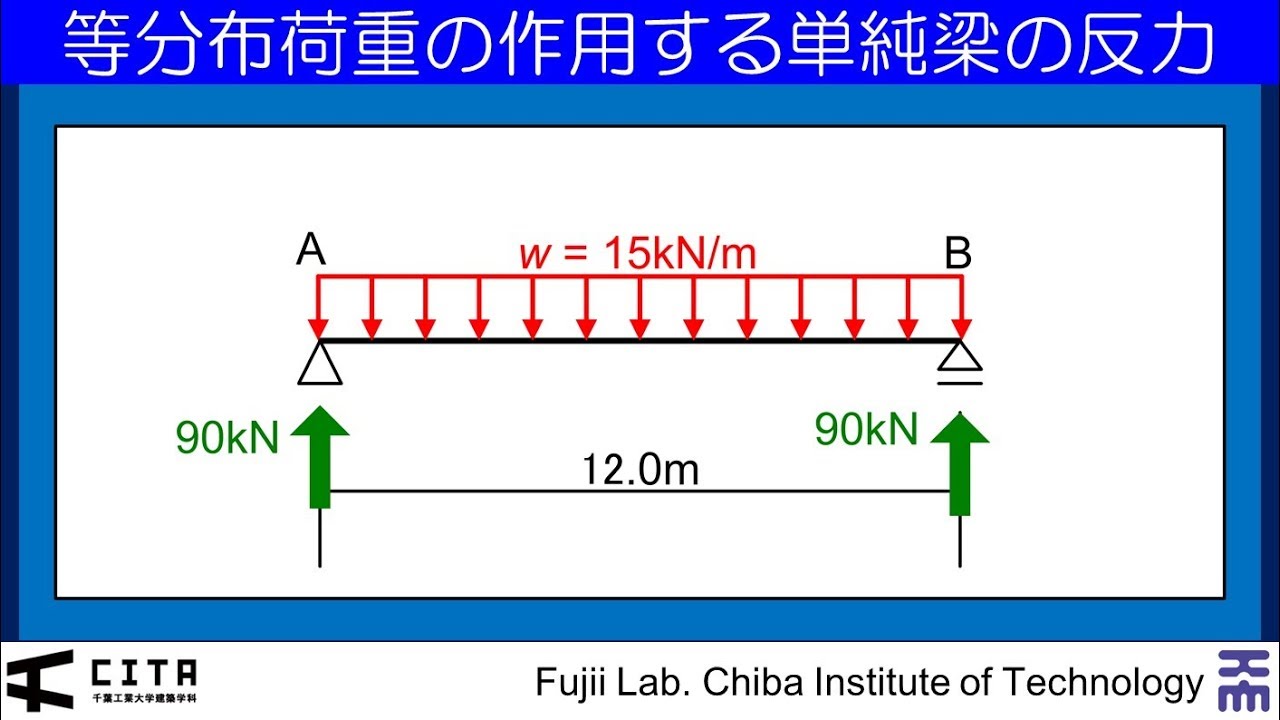



構造力学入門 反力編03 単純梁3 Youtube
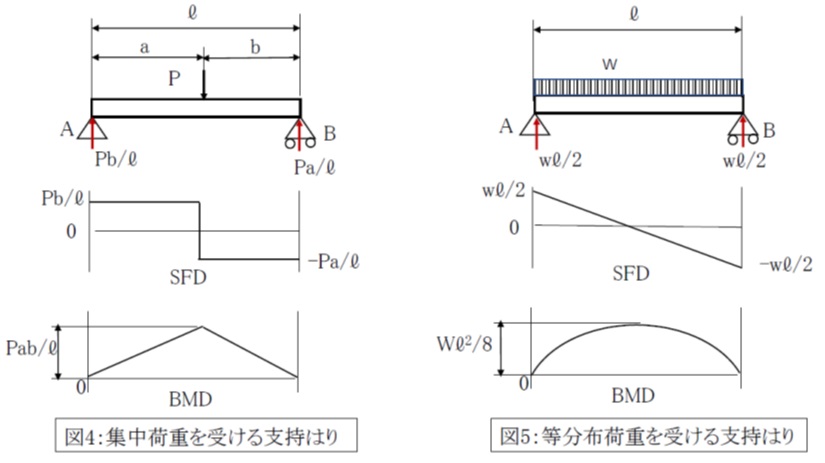
4)両端固定梁で等分布荷重 5)片持ち梁で先端集中荷重 6)片持ち梁で等分布荷重 Ⅱ:他のプログラムと比較する ここでは、spaceを使用して解の比較を行う 1)中央集中荷重を受ける単純梁 次に、例題として、上に示した単純梁で中央集中荷重の解析結果をL:荷重図 Q:せん力図 M:曲げモーメント図 W:全荷重 M:曲げモーメント R:反力 θ:回転角 Q:せん断力 δ:たわみ 両端固定 中心荷重 両端固定 偏芯荷重 両端固定 等分布荷重 kanpro 公式集-梁等分布荷重を受ける両端固定はり・理論解 中原,実践材料力学,p85 例題3 参照 (1) Fig1 に示すような両端を固定されたはりに等分布荷重を加える.このときはりに発生する ①曲げモーメント,
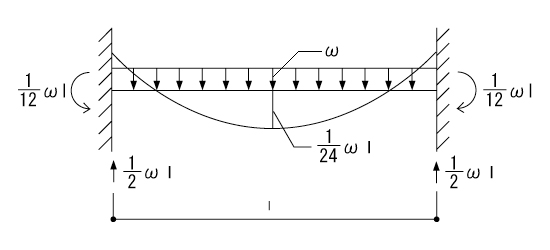
両端固定梁曲げ応力計算例H300、等分布荷重 構造力学 曲げ応力の検討 1.最大曲げモーメントの算出 最大曲げモーメントM = 単位荷重p × スパン長L² ÷ 12 単位荷重p : 1kN/m スパン長L : 10m 最大曲げモーメントM = 1kN/m × 10²m ÷ 12 =梁公式集 1片持梁 2単純梁 3はね出し単純梁 41端ピン他固定 5両端固定梁 6連続梁 7三角形の面積 携帯用壁紙 240×3用, 2スパン等分布荷重と両端にモーメントが同時に作用 EI wl M M EI EI wl M M EI B A A A B 24 2 6 τ 24 2 6 τ 3 3 モーメントを求める式に変換 中間荷重が無 い場合と同じ 中間荷重が作用し た時の固定端モー メント 12 wl2 12 wl2 固定端:τA
図の梁の場合に、たわみの式と自由端のたわみを求める。弾性係数と断面二次モーメントをe、iとする。 解答例 問題252 図のように、段付き丸棒が、両端a,bにて剛体壁に固定されている。丸棒の中央cに図のようにトルクt=3dpが作用している。両端固定梁及び単純梁モーメント 基本的な両端固定梁モーメント 基本的な両端固定梁の等分布荷重と集中荷重のモーメントを求める公式は次のようになります。 等分布荷重時 両端M=(1/12)wl 2 中両端支持のたわみ計算は、荷重条件と支持条件で変わります。集中荷重が作用する単純梁のたわみ=pl 3 /48eiです。 等分布荷重が作用する単純梁のたわみ=5wl 4 /384eiで求めます。 今回は両端支持のたわみ計算、公式、両端固定梁のたわみについて説明します。



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ




わかりやすい 詳細 等分布荷重を受ける単純支持はりのたわみ
計算を実行すると、梁のたわみ量(mm)、応力(MPa)、重量(kgf)が出力されます。 Step1 梁の支持方法を選択します。 片持ち 両端支持 両端固定 集中荷重 等分布荷重 片持ち|集中荷重 Step2 断面を選択します。 ここにない単純梁の曲げモーメントは? 1分でわかる求め方(計算)、公式 曲げモーメントの公式は? 1分でわかる公式、導出、両端固定 曲げモーメントの公式では、wl 2 /8、wl 2 /12を必ず覚えてください。 構造設計の実務では、Mo(えむぜろ)、C(しー)という値図の梁において、固定点bに生ずる反力と反モーメント、sfd,bmdを求める。 解答例 問題316 図の梁において、梁の中央cd=bに等分布荷重wが作用する。せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。



はりの話 前編
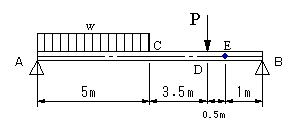



Ex 2
元の等分布荷重を受ける片持ちはりのフリーボディダイアグラムは図 612となる。 図612 等分布荷重を受ける片持ちはり 図612から,固定端Aでの反力RA とモーメントMA を求める。力のつ り合いから, RAA ql R ql0 (611)等分布荷重が作用する梁のモーメントの値として、「wL 2 /8」「wL 2 /2」があります。 等分布荷重は単位長さ当たりの荷重です。よって、モーメントの式は「wL 2 /〇」となります(〇の値は荷重条件、支持条件で変わる)。 今回は等分布荷重によるモーメントの求め方、公式、片持ち梁との関係単純梁と両端固定梁を比較単純梁の方が変位が大きい 最大せん断力については集中荷重・等分布荷重どちらも同じである。 荷重を負担するのが両端2箇所で同じであるため、同様の値となる。 最大曲げモーメントはどちらの荷重条件でも単純梁のほう



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ



両端支持のたわみ計算は 1分でわかる計算 公式 両端固定梁のたわみ
各種梁の荷重条件別の計算式の見出し(計算式は次ページ以降) 圧 力 3d参照 ====== はねだし単純梁 ====== 2スパンの連続梁 支持 固定 固定 支持 短銃ん支持 案内付 固定 固定 自由 片持ち梁 梁の タイプ 荷重の タイプ 集中荷重 等分布荷重 偏心両端固定中心荷重 両端固定任意等分布荷重 両端固定等分布荷重 両端支持 両端固定 δ = pl 3 3ei ≒ 45 δ = 800×500 3 3××1054×10 4 例 フレーム:sf240・40 l=500 p=800n δ = 1 pb 3ei 3a 2b ( ) 1 4梁の図面と計算式 オメガエンジニアリング 梁の図面と計算式 (続き) 圧力 49 両端支持梁 全長に均等 荷重 荷重 せん断 力 モーメント 中心では x 両端固定梁の場合 次の 例題は図441の両端固定の 場合であるが,この場合にも例えば図示したような三つの静定系の
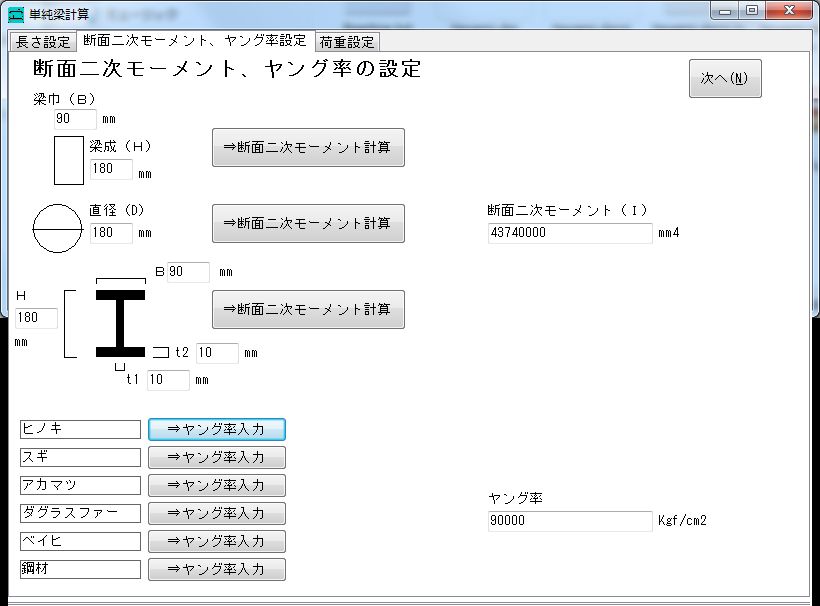



単純梁の構造計算 せん断 剪断 曲げモーメント たわみ 撓み 計算 無料フリーソフトダウンロード



棚板の耐荷重の考え方と 耐荷重計算のやり方を解説します とある建築士の憂鬱
等分布荷重の作用する梁の公式は、曲げモーメントM=wL 2 /8、たわみ=5wL 4 /384EIで計算します。 両端が固定支点の場合、曲げモーメントM=wL 2 /12、たわみ=wL 4 /384EIです。 今回は、等分布荷重が作用する梁の計算と公式について説明します。基礎64話 No2 両端固定梁+等分布荷重 少し複雑な不静定構造のたわみと断面力 基礎65話 No1 一端固定・他端ピン支持梁+等分布荷重 基礎66話 No2 一端固定・他端ピン支持梁+中央集中荷重33 曲げを受ける部材の強さ 331 はりに作用する力 (1) はりの種類 ・片持はり(ばり) 一端が固定されているはり
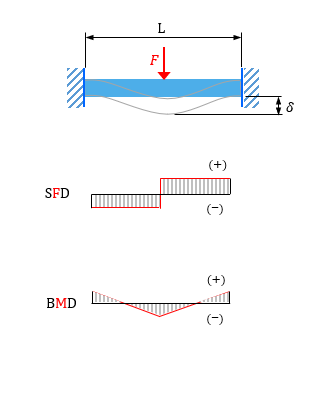



梁のたわみと応力計算ツール



第8章 構造解析法への適用
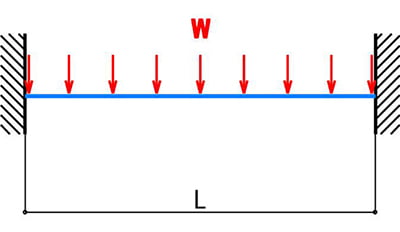
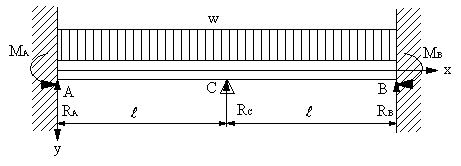
はりの強度計算 両端固定ー等分布荷重ー長方形 製品設計知識 HOME > 設計者のための技術計算ツール > はりの強度計算(応力・ひずみ・たわみの計算) > はりの強度計算 両端固定 > はりの強度計算 両端固定ー分布荷重 >前回の続きで、図4に示す両端固定支持梁に等分布荷重が加わる場合 の応力解析を行う。等分布荷重 p w を受ける梁の微分方程式は、 1 で与えられ、上の両辺を4回積分すると、 dx 32 1 2 34 となる。境界条件として、梁両端が固定であることより、以下の4つの直荷重Pが作用した場合、A、C点の鉛直反力の絶対値として、正 しいものは次のうちどれか。ただし、梁は等質等断面とする。(H5) 2l0 2 40l p a c b 過去問56 同じ単純梁が等分布荷重wおよび集中荷重Pを受け る場合の梁の中央の鉛直変位が ei wl a 384 5 4 g



Www Jp Omega Com Techref Pressure43 67 Pdf
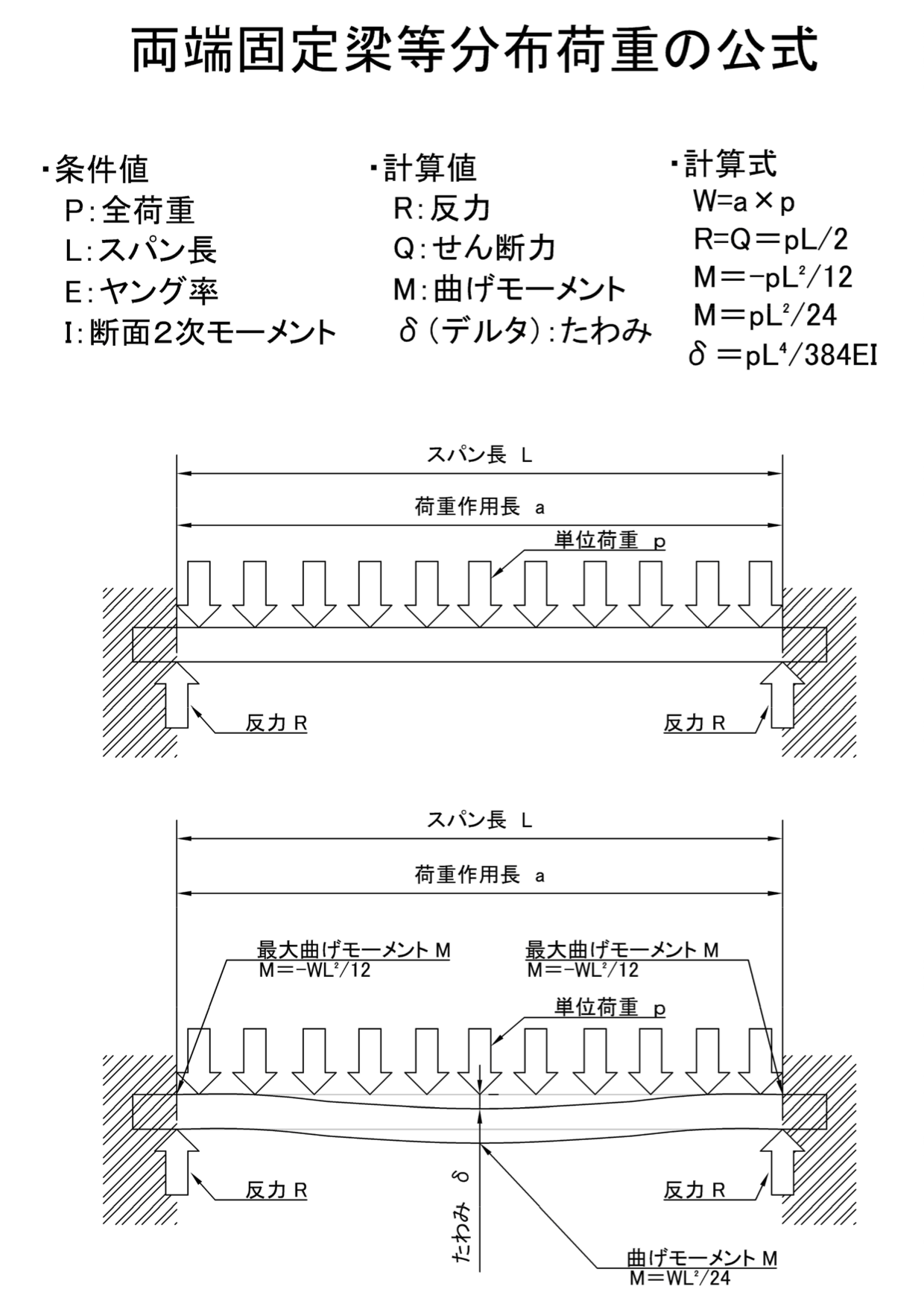



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督
材料力学の典型的な問題 PartⅠ 米国公認技術者資格 (PE/FE) の試験問題は英文ですが、材料力学の問題は、公式を3つか4つ組み合わせて解くようなものが多くあります。 「はじめての材料力学」 (森北出版)では材料科学の知識を導入し、変形を考察し、数式材料力学ii 演習課題(第5 章分) 1.下図のように部分的に等分布荷重w を受ける片持ち梁のたわみ曲線および自由端のたわみを求めよ. ただし,はりの曲げ剛性をei とする. 2.下図のように自由端に集中荷重を受ける段つき片持ち梁がある.ac 間で曲げ剛性がei,bc 間でnei等分布荷重を受ける単純支持はりのたわみ曲線は,上に凸の四次関数で表される。 また,たわみの最大値 ymax y max は次式のとおり 217 mm となる。 ymax = 5ql4 384EI z = 5×1× 384×0,000×3,000 = 217 mm y max = 5 q l 4 384
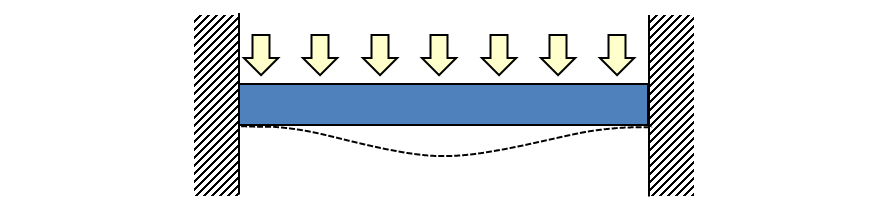



はりの強度計算 両端固定ー等分布荷重ー長方形 製品設計知識



両端固定梁のたわみ 応力 支持反力 集中荷重
• 荷重は,集中荷重や等分布荷重などに 作用する荷重・支え方などの外的要因 • いくら荷重をかけても劣化しない,変形はわずか 用いる材料の特性や変形・変位集中荷重 等分布荷重 梁は変形 しない棒に (建築では,積載荷重,固定荷重) 27 つり合い,静定と不静定,安定と不安定 静止している構造物(つり合い) • 並進運動も回転運動もしないこと. 両端固定梁せん断応力計算例H300、等分布荷重 構造力学 せん断応力の検討 1.最大せん断力の算出 最大せん断力Q = 単位荷重p × スパン長L ÷ 2 単位荷重P:1 kN/m スパン長L:10m 最大せん断力Q = 1kN/m × 10m ÷ 2 =5kN



すみませんが また構造力学の質問が出てきました 下記の図 b Yahoo 知恵袋



梁のたわみと応力計算ツール
計算を実行すると、梁のたわみ量(mm)、応力(MPa)、重量(kgf)が出力されます。 Step1 梁の支持方法を選択します。 片持ち 両端支持 両端固定 集中荷重 等分布荷重 片持ち|集中荷重 Step2 断面を選択します。 ここにない両端固定梁 等分布荷重の作用する両端固定梁のせん断力qは下式で算定します。 いずれの場合も等分布荷重wとスパンlの積に比例する点は変わりません。 まとめ 今回は等分布荷重によるせん断力の求め方について説明しました。梁のたわみと応力計算ツール 利用方法 Step1:梁の種類を選択 Step2:断面の種類を選択 Step3:材料を選択 Step4:各数値を入力 計算を実行すると、梁のたわみ量 (mm)、応力 (MPa)、重量 (kgf)が出力されます。 Step1 梁の支持方法を選択します。 片持ち
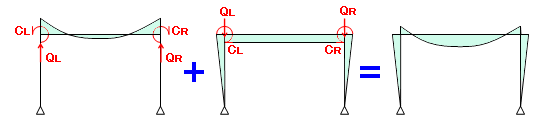



中間荷重の処理
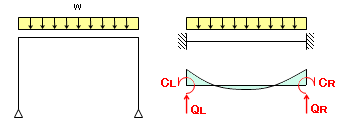



中間荷重の処理
両端回転自由 長方形断面 一端固定、他端自由 両端固定 たわみ・応力 片持ち梁(一様断面) スプリング 集中荷重 コイルスプリング(円形断面) 等分布荷重 たわみ 2点支持梁(一様断面) 荷重 集中荷重 トーションスプリング(円形断面) 等分布単純 偏芯集中荷重 単純 等分布荷重 単純梁 両端ピン ← 図をクリックすると、 各種計算式が表示されます。 反力、せん断、曲げモーメント、 たわみ、・・・ Type ピン-固定 中心集中荷重 ピン-固定 偏芯集中荷重 ピン-固定 等分布荷重 ピン 固定梁1122 等分布荷重 を受ける両端固定 梁 図114 等分布荷重を受ける両端固 定梁の断面力分布と変形状態 EI:一定z Pw 2 12 −PLw 2 12 −PLw 2 24 PLw 2 PLw 2 −PLw 4 max 384 w z PL w EI = (a) 等分布荷重を受ける両端固定梁 (b)



アプリ開発 マルイ設計コンサルタント



はり公式集p3
3)等分布荷重の種類 ・部材自重 ・上記活荷重 ・群集荷重 ・土重 ・舗装 新たなソフトを追加しました。 三辺固定版(三角形分布荷重、台形分布荷重)構造計算です。 8-6 三辺固定版三角形分布荷重(大型構造物側壁等)集中荷重が作用する単純梁の曲げモーメント ⇒ M=αwL 2 等分布荷重が作用する単純梁の曲げ 両端固定梁及び単純梁モーメント 基本的な両端固定梁モーメント 基本的な両端固定梁の等分布荷重と集中荷重のモーメントを求める公式は次のようになります。両端固定版の構造検討(頂版) U型構造物のような両側側壁に頂版を固定した場合、その上に群集等の等分布荷重が載るコンクリート版 両端固定の構造計算を行う。 1.プログラムの内容 1) 等分布荷重載荷によるコンクリート版両端固定の構造計算。



棚板の耐荷重の考え方と 耐荷重計算のやり方を解説します とある建築士の憂鬱



等分布荷重によるモーメントは 1分でわかる求め方 公式 片持ち梁との関係



今月のまめ知識 第10回 有効に 剛性 を出す組合せ Nic アルファマガジン Com



両端固定はりのたわみ計算 はりのたわみ計算 オンライン



2点集中荷重が作用する両端固定梁の公式は 1分でわかる求め方 解き方 と計算




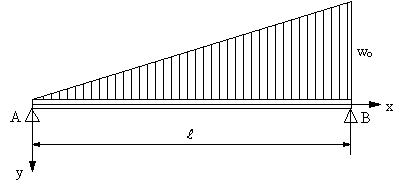
わかりやすい 詳細 三角形状分布荷重を受ける片持はりのたわみ




単純梁の曲げモーメント 計算 分布 関係



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社
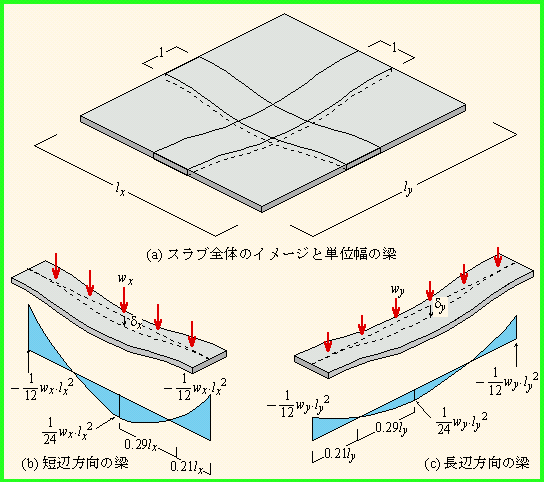



8 2 周辺固定スラブ



材料力学の問題です 下図のように両固定端の梁に等分布荷重がかかっていま Yahoo 知恵袋




両端支持梁に集中荷重 2か所 の場合の最大応力 両端支持の梁に2か所 物理学 教えて Goo



4 1 梁の境界値問題



たわみ 等 分布 荷重
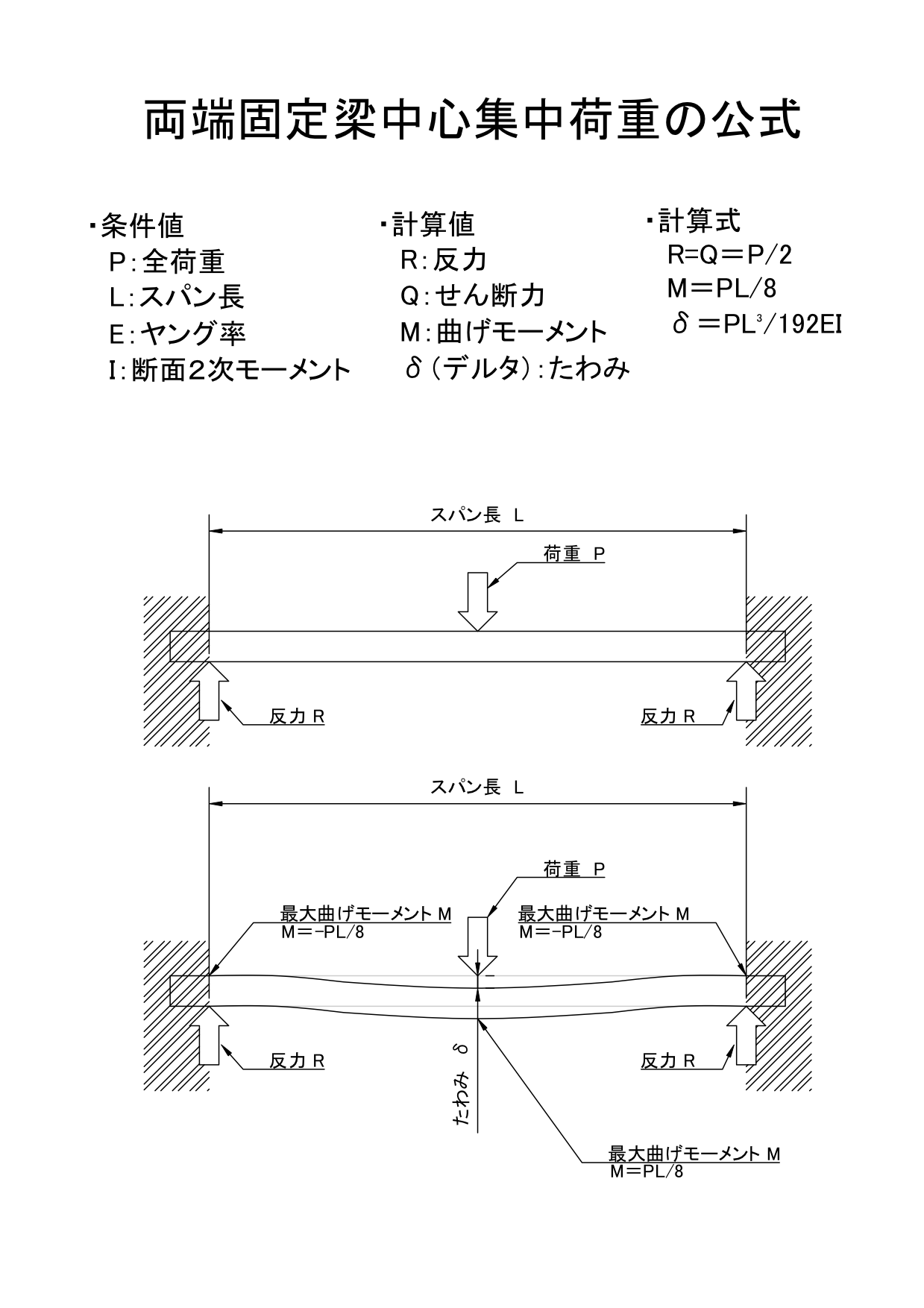



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督



Http Tass2x4 Sakura Ne Jp Sblo Files Tass2x4 Image E59fbae7a48e 64e8a9b1efbcbfe4bde99d99e5ae9ae381aae59fbae69cace6a78be980a0e381aee5bf9ce58a9be8a7a3e69e90no2 Pdf
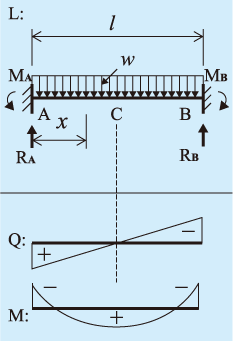



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社
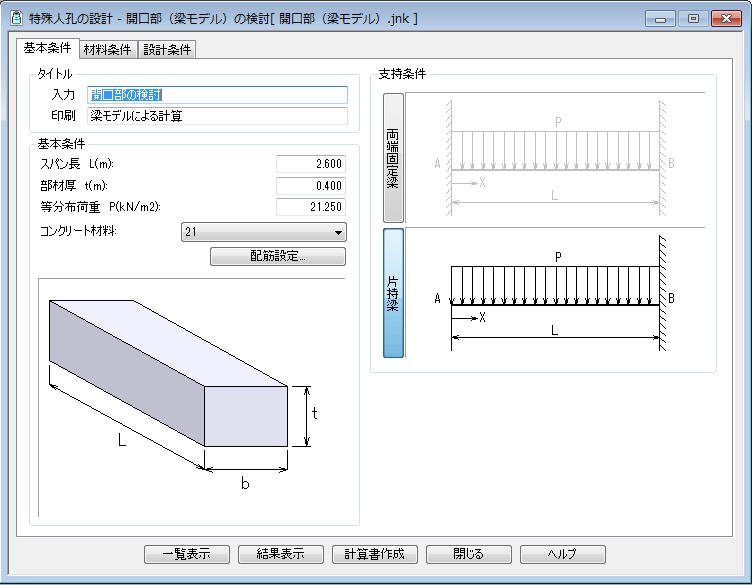



製品情報 株式会社シビルソフト開発



種々のはりのたわみ
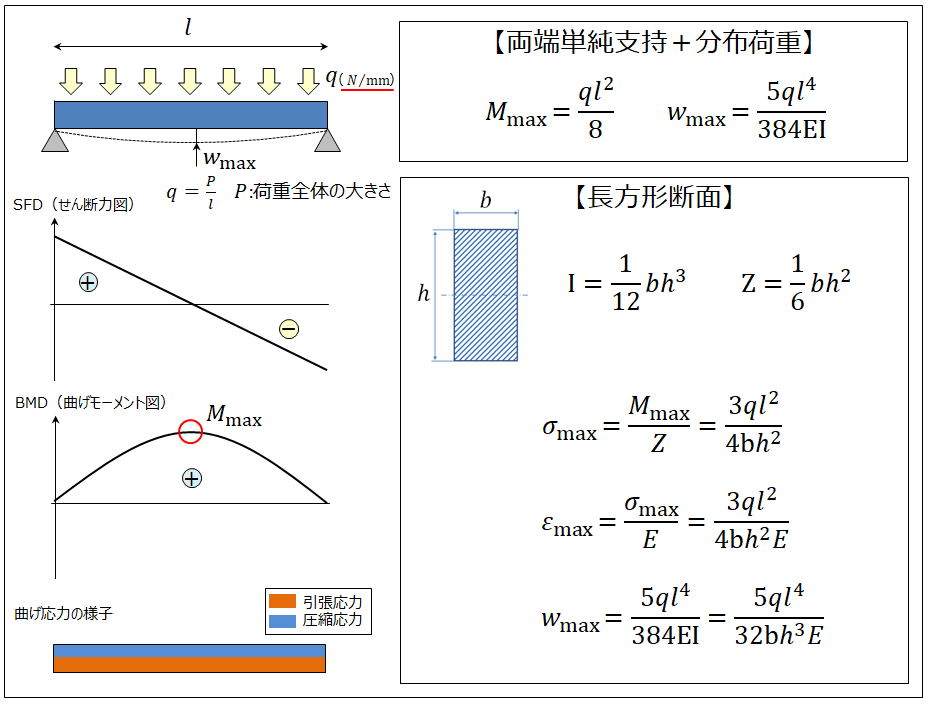



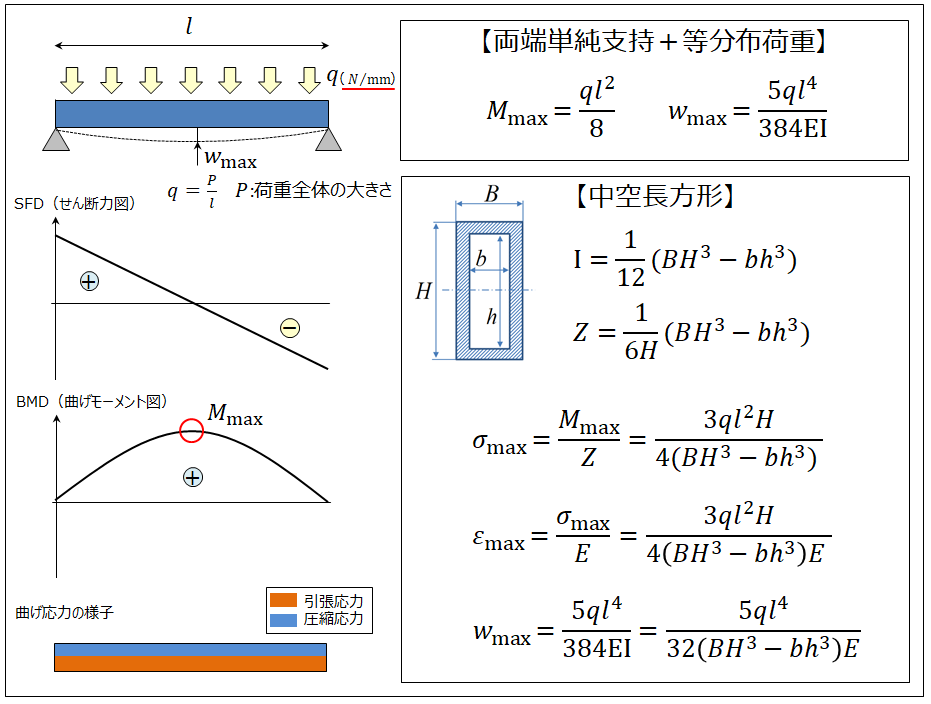
はりの強度計算 両端単純支持 等分布荷重 長方形 製品設計知識
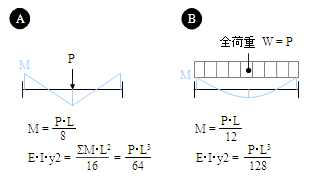



梁のたわみ量の計算について




わかりやすい 詳細 等分布荷重を受ける単純支持はりのたわみ




梁の計算7 両端固定梁 等分布荷重 Youtube



はり公式集p2



はりの話 前編




わかりやすい 詳細 三角形状分布荷重を受ける単純支持はりのたわみ



今月のまめ知識 第36回 アルミフレームのつなぎ方 Nic アルファマガジン Com
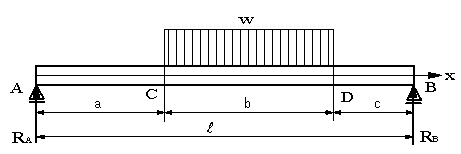



Ex 5



よくでる不静定モーメント 構造力学 Com




梁のたわみ量の計算について



Step1 1




材料力学 梁 はり の分布荷重の計算方法 公式通りの積分で簡単に解けるよ のぼゆエンジニアリング



4 1 梁の境界値問題



Ex 5



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ



曲げモーメント せん断力 たわみの計算式 県木連のホームページ 一般社団法人愛知県木材組合連合会
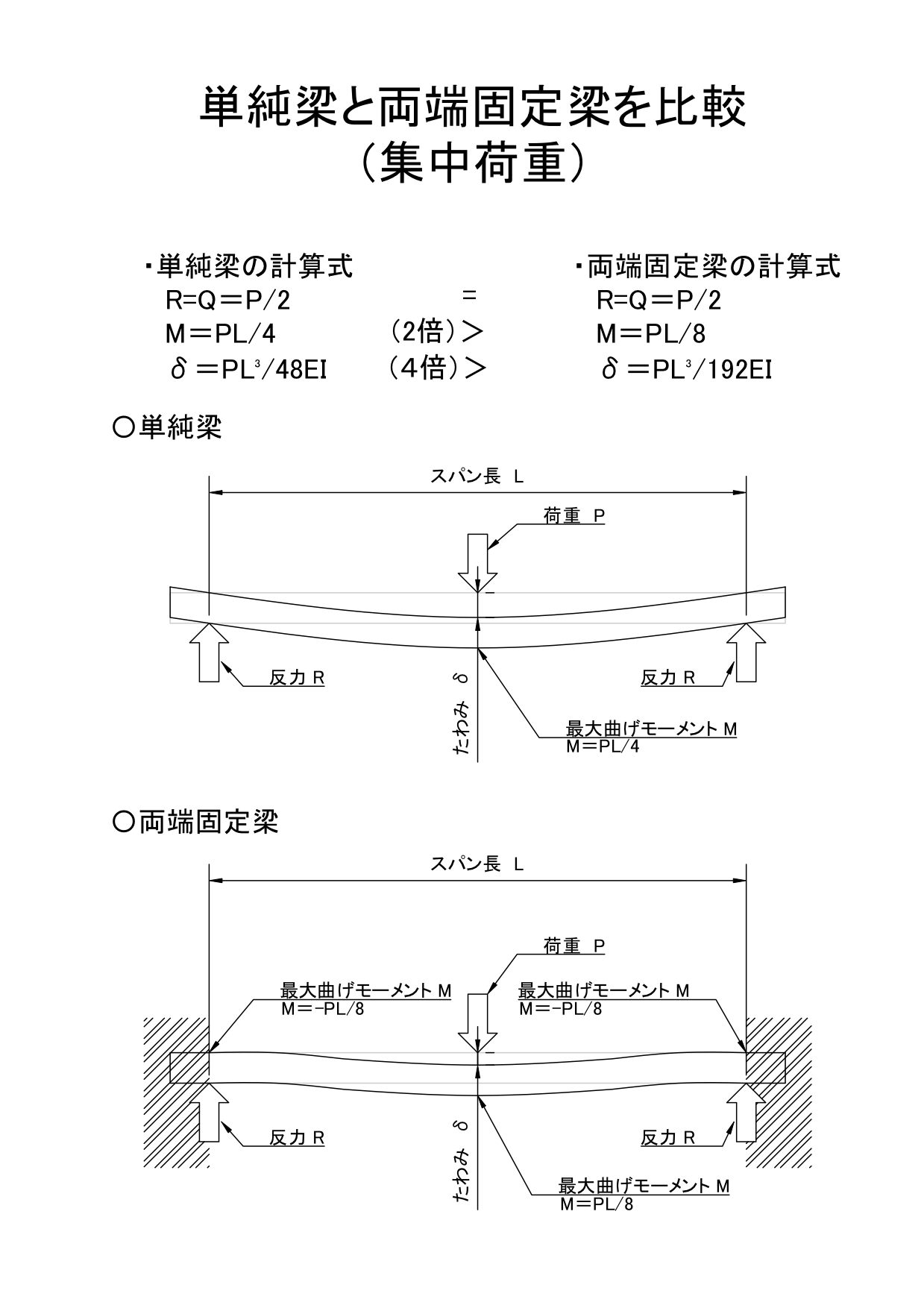



単純梁と両端固定梁を比較 単純梁の方が変位が大きい 機械卒でも土木の現場監督




構造力学入門 反力編03 単純梁3 Youtube



Www Jp Omega Com Techref Pressure43 67 Pdf




材料力学静定梁両端固定の最大たわみ 材料力学の静定梁の問題です 両端固定 Okwave



Autodesk Inventor オートデスク インベンター の使い方




梁の計算7 両端固定梁 等分布荷重 Youtube
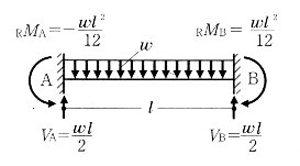



不静定ばりの応力解答 構造力学 Com



等分布荷重の計算と公式は 1分でわかる公式 計算方法 反力の求め方
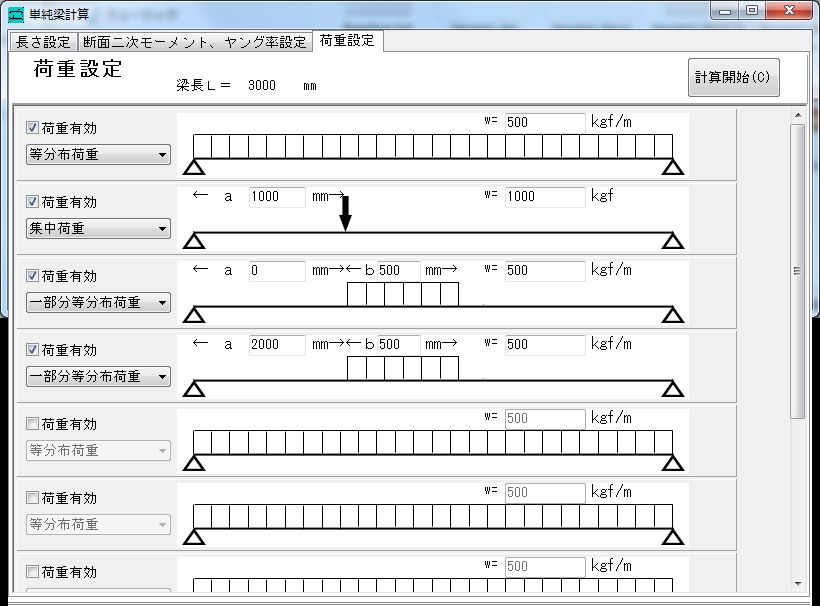



単純梁の構造計算 せん断 剪断 曲げモーメント たわみ 撓み 計算 無料フリーソフトダウンロード




M Sudo S Room 単純支持部分三角荷重梁の計算 両端固定も記載



アプリ開発 マルイ設計コンサルタント
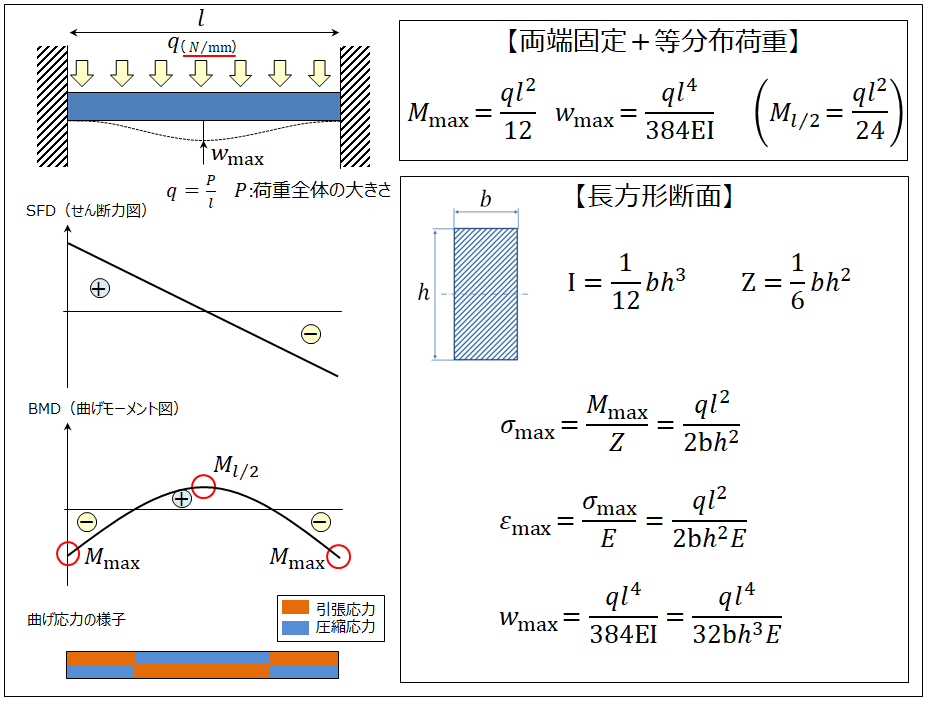



はりの強度計算 両端固定ー等分布荷重ー長方形 製品設計知識



画像の等分布荷重を受ける両端固定梁のa点及びb点に生じるモーメ Yahoo 知恵袋
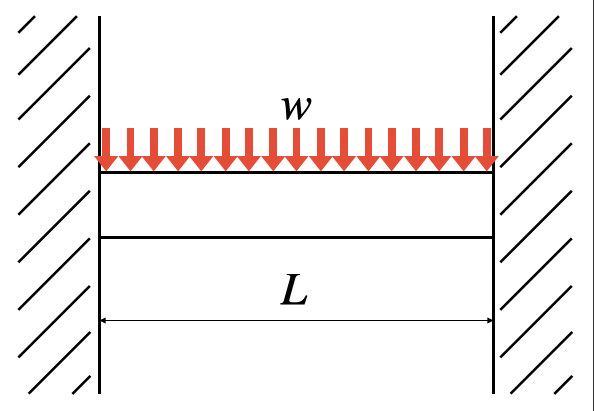



梁 反力 曲げモーメント たわみ 曲げ応力 公式集 計算ツール ものづくりのススメ
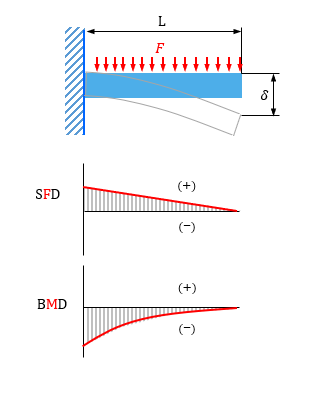



梁のたわみと応力計算ツール



単純 梁 片 持ち 梁
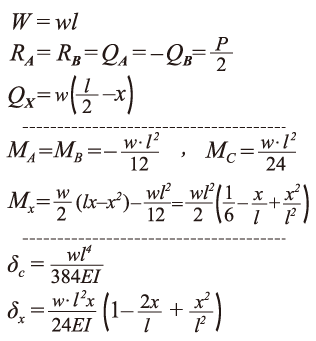



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社




04 はりの曲げ 基礎および分布荷重が作用するとき等 材料力学の事前 事後学習課題作成のヒント



曲げモーメントの公式は 1分でわかる公式 導出 両端固定 単純梁 片持ち梁




仮想仕事の原理による梁のたわみの計算例 バッコ博士の構造塾



機械設計マスターへの道 はり の基礎知識を習得 Sfdとbmd たわみの計算方法は アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション



はり公式集p1




両端固定はりのせん断力と曲げモーメント 図のような固定はりのせん断力 曲 Okwave



Ex 7



両端固定梁のたわみ 応力 支持反力 集中荷重



公式集 構造計算 両端固定梁 曲げモーメント せん断 反力 たわみ



Kenchikuchishiki Com Wp Content Uploads 16 07 Harimoumento6 Pdf



鉄筋コンクリート梁の配筋の要領は 配筋の基礎を紹介 建築学科のための材料力学



Www Jp Omega Com Techref Pressure43 67 Pdf
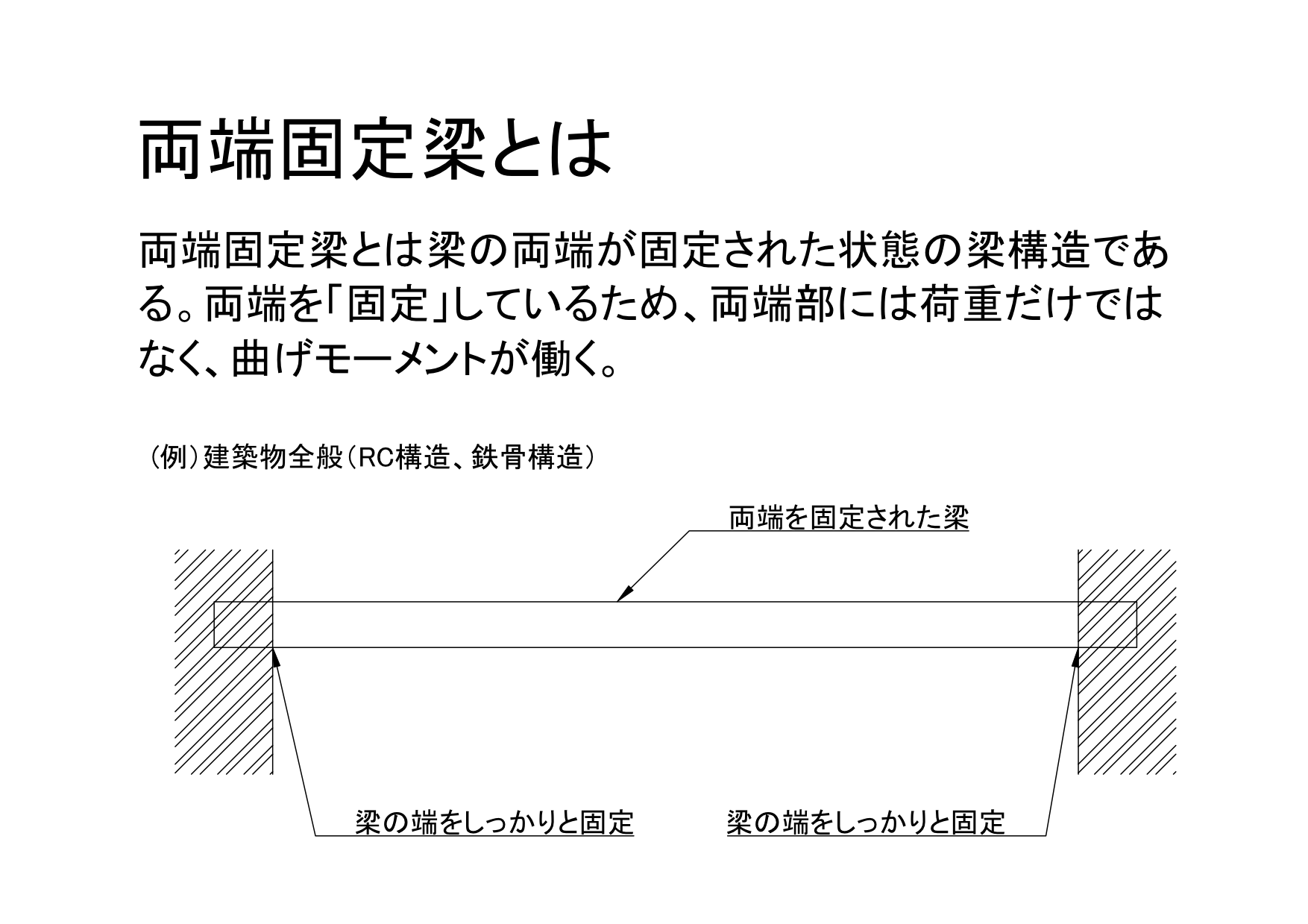



両端固定梁とは 梁の両端を接合 機械卒でも土木の現場監督



単純梁の計算公式 任意長さ等分布荷重



Seihin Sekkei Com Wp Content Uploads 17 08
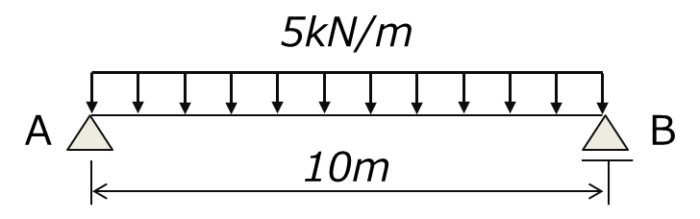



構造力学 断面力図の問題その1 分布荷重
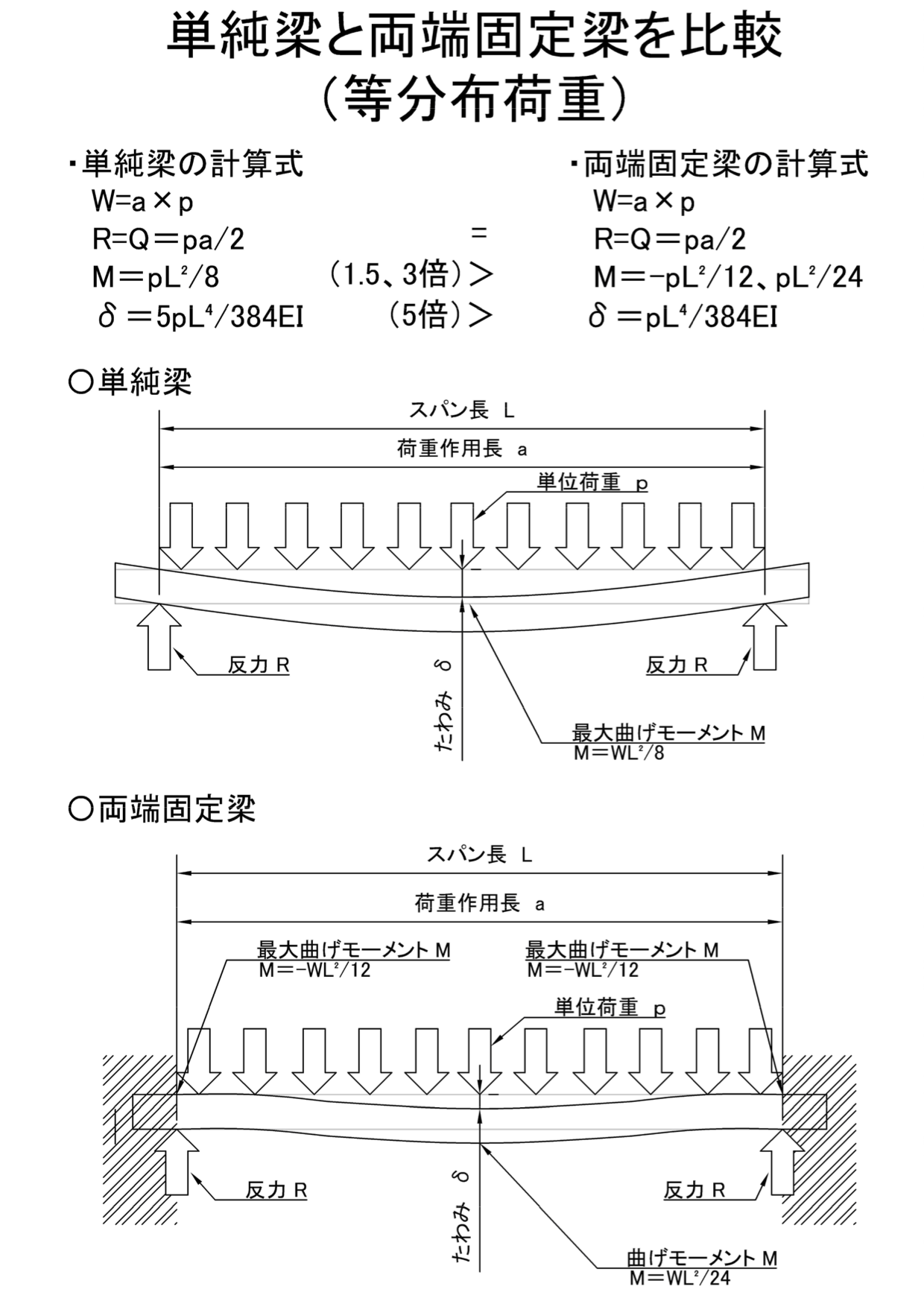



単純梁と両端固定梁を比較 単純梁の方が変位が大きい 機械卒でも土木の現場監督
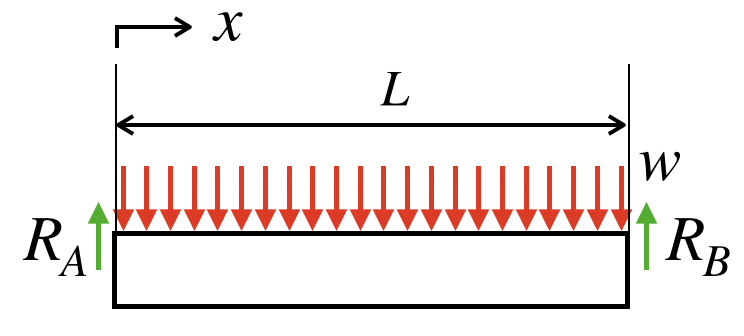



計算を簡略化 等分布荷重のsfd Bmdの書き方 ものづくりのススメ




1 2 静定構造の反力計算と応力計算 1 2 1 単純梁と片持ち梁 1 2 2 荷重の種類について とある若手構造設計者の徒然blog
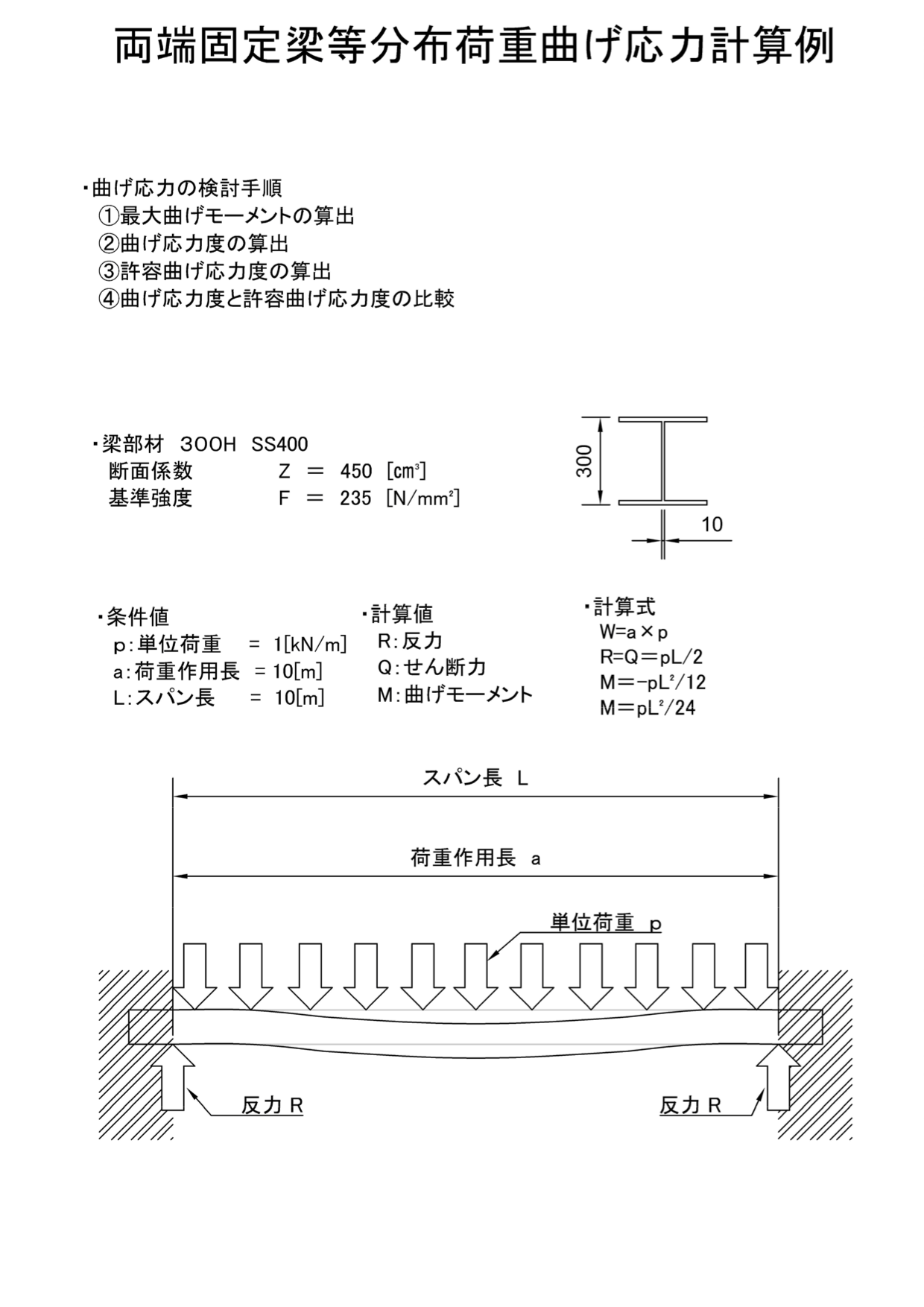



両端固定梁曲げ応力計算例 H300 等分布荷重 機械卒でも土木の現場監督



梁のたわみを求める 単純梁 等分布荷重



両端固定分布荷重で距離aの位置からbの幅で等分布荷重がかかっている時 xの Yahoo 知恵袋



許容応力度とたわみによる断面算定の考え方 県木連のホームページ 一般社団法人愛知県木材組合連合会
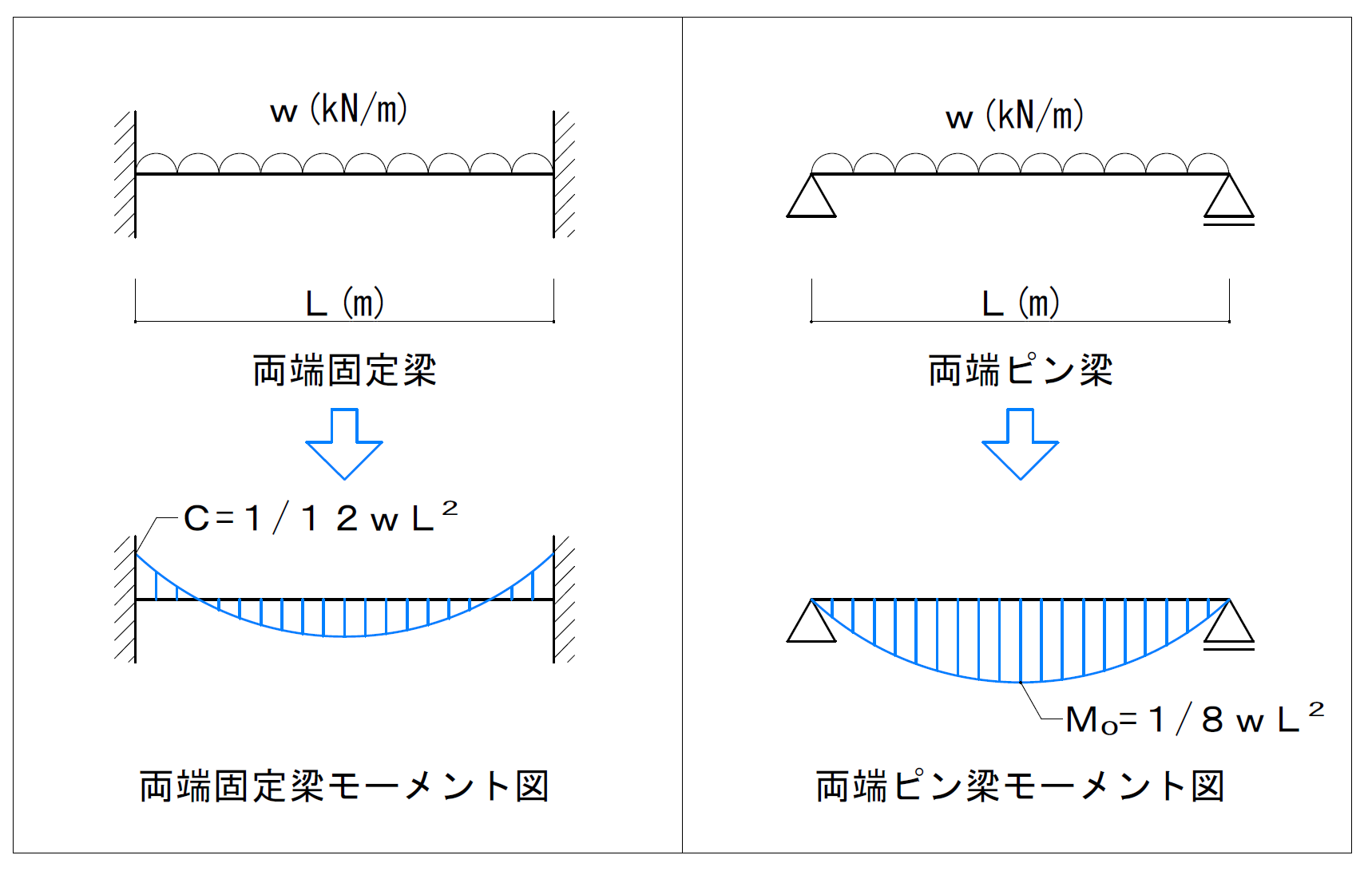



小梁の設計 C M Qとは 構造設計memo




M Sudo S Room 両端固定部分等分布荷重梁 の計算




一級建築士試験で覚えておくたわみとたわみ角の覚え方 建築士試験の勉強法



レポート 有限要素法解析で見る材料力学 2
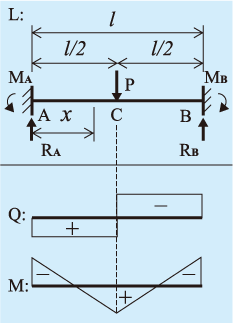



構造計算 両端固定梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社



0 件のコメント:
コメントを投稿